
Subsequently, I've had chance to meet statisticians who currently work on RaiseOnine, who seem to be well aware of the issues which I raise here. Unless and until I get time to revise the piece thoroughly, I plan to leave it here. Raise still uses significance testing in a way which is at the very least highly misleading, and is at worse, contemptuous of the hard working staff in schools across the country which have been unfairly pilloried by those who simply don't understand how data works.
If you like to find out how RaiseOnline can be useful, as well as learning how to make sure that no-one misrepresents your school using the information it contains, I'm running some CPD in January 2015. In the meantime, your thoughts are welcome in the comments.)
Having had a good look at the Ofsted Schools Data Dashboard and the DfS’ Performance Tables, it’s time to take a look at RAISEonline, the slickly acronymed behemoth of the Big Data Disaster. In full, RAISE is actually ‘Reporting and Analysis for Improvement through school Self-Evaluation’. It may as well be called Reporting Utter Bollocks Because It’s Simply Hogwash. It is based on bad statistical analysis, is hopelessly misleading and has been used unbelievably badly by those who should know better.
Part of the issue with RUBBISHonline is that it requires some fairly entry level statistical knowledge to understand what you can and cannot infer from data analysis. Those who developed RUBBISHonline into the sense-eating monstrosity it has become has taken some quite clearly misunderstood statistical theory and, in effect, added two and two to make a banana.
Having pored over the statistics behind RUBBISHonline, I'm still somewhat shocked at what I have discovered. It seems so incredible that the analysis is so wrong, and I have gone over the arguments I make here over and over, convinced that I must have missed something. I did in fact make few mistakes in the initial version of this article, as I managed to confuse the distributions of raw data and the means of samples of data as very helpfully pointed in the comments below.
I am convinced, however, that my basic criticisms of RAISEonline stand, and I welcome any further comments you may have.
This post is likely to patronise you, scare you and infuriate you in equal measure. But in order to understand why RUBBISHonline has been and continues to be so damaging, you need to look the maths in the face and not be intimidated by people wielding bad data as a weapon. You need to understand how the good name of statistics has been besmirched. And you need to take a stand against crimes against statistics, schools and children.
Bear with me whilst I patronise you a bit
Now, as I have previously said, I have studied Statistics to a high level. And whilst this doesn’t make me the Data God, it does give me a leg up when it comes to explaining a bit about the way statisticians work with data. So bear with me as I give you a bit of an insight into what those working with data have developed to try to make sense of what you can, and can’t, do with data. Apologies if you do understand all this. In my ten years’ experience in Primary education I’ve yet to meet anyone who has studied this in any depth, so I’m going to assume that you have not done so either. If you have, feel free to skip this bit and rejoin the post below when I outline some headline problems with RUBBISHonline.
So firstly, I’d expect most people to have a rough idea of what a normal distribution looks like, even if you are not used to that term. It’s the big hilly graphy thing which tells you that, most things in a given set of data are somewhere in the middle with some on either side. A ‘Bell’ curve. One of these:
Of course, I’m using ‘sample’ and ‘population’ in their statistical sense, but you wouldn’t know that because they are English words and were used originally because, well it made sense not to make up new words like ‘spingle of data from a bygoat’. This will become important a bit later on…
The mathematical thinking behind this distribution of means is made explicit in the Central Limit Theorum, which states that, with various important provisos, the means of independent and identically distributed random variables are themselves approximately normally distributed.
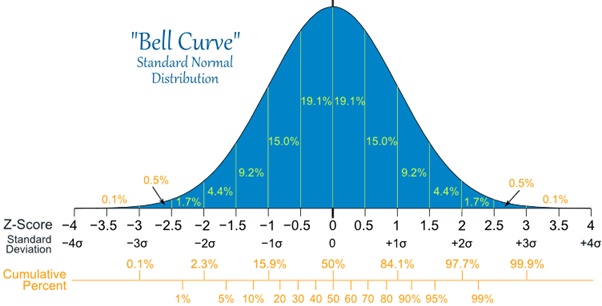
So what a statistician will do is to transform the data under investigation into an imagined distribution of means, which looks like this:
Most of the graph is clustered around the middle of the distribution.
- The percentages refer to the areas under the graph.
- The further you get from the middle, the smaller numbers are.
- The ‘z-scores’ or ‘standard deviations’ are a simple but beautiful bit of mathematical trickery which allow you to look at the spread of data around the middle value.
- Just over 68% of the graph is between -1 and 1 standard deviations from the mean.
- Just over 95% of the graph is within 2 standard deviations from the mean.
- Just over 99% graph is within 3 SD from the mean.
Fairly straightforward, really. Except for the last three points, which get a bit more specific and math-y. But that’s what those studying science at university learned about whilst the arts grads discussed poetry and whether trees in the forest make any sound when they fall over for reasons which never seem to be explained or considered important. Ahem. I digress.Anyway, what all this allows statisticians to do is to crunch numbers and perform tests to see if a given statistically valid sample of a population is different to another statistically valid sample of a population.
A push and shove and this land is ours
I know, know, your head probably hurts (I did mention the patronising above, didn’t I?). A bit more stat-stuff before we can have a good took at RUBBISHonline. Bear with me once again.
So, statisticians collect data from a random sample of the population under scrutiny and find its mean, by adding up all the numbers and dividing the total by the number of observations. Then they test it to see if it is different to a mean of another random sample.
It’s worth pointing out that, and Statisticians use ‘population’ to mean ‘the group being studied’ and sample ‘sample’ to mean ‘completely random sub-section of the population.’ By collecting data on, say, a completely random group of a surprisingly small number of people over the age of 18 in England, you can be fairly certain that your data will give you enough data to start to generalise about adults over 18 in England.
Here comes the very large and important ‘BUT’
There are a few major issues with this kind of generalisation, however.
- Firstly, you need to be fairly sure that the means of your data are actually normally distributed, i.e. are actually evenly distributed around the most common value.
- Secondly, you need to be fairly sure that your samples contain independent and identically distributed (IID) random variables.
- Third, your population has to be fairly accurately defined, since adults over 18 in England may be quite different to, say, adults over the age of 18 in Japan.
- Finally, you need to understand that your population is a theoretical construct containing all the people who you might have had in your sample if the time and money involved weren't prohibitive. Not, the actual population.
If all these things are understood and you feel you can make these generalisations, then you can use some funky maths to find out if a new sample of adults over 18 in England is similar to your first sample or not. The great thing about the maths for this is that it is designed for people who don’t really need to understand the maths. You just measure something about people, find the mean and standard deviation of the sample, and put these into a simple equation which includes the mean and standard deviation from your first sample.
This gives you a number – the Z-score on that last scary graph - and if that number is between two given values, you can be fairly sure that your two samples are ‘statistically similar’. If they are not similar, statisticians say that the comparison between them is ‘significant’. To a Stat-head, this means that they might not be drawn from the same population. It doesn’t mean that they are definitely different. It simply means that the maths says that you might want to look closer to see what is going on.
You’ve probably even seen these Z-scores, if you’ve looked closely at any data. Does 1.96 ring any bells? If it does, it’s because 95% of values in a normal distribution occur between -1.96 and 1.96 standard deviations from the mean.
Anyway, here endeth the lesson. You should now have been thoroughly patronised, may be a little scared, but you should have a rough idea how statisticians calculate Z-scores for standardised normal distributions. Let’s get back to the abuse of data.
RUBBISH data analysis always starts with the best of intentions
Back to RUBBISHonline. So, it will all have started with someone wanting to know how children in school are progressing. I think most people would agree that it is worthwhile trying to work out whether children are developing as they move through school. That’s why we try to assess what children know in increasingly formal ways as they get older. I teach in Primary, and it is useful to know roughly how children are getting on with the core skills of reading, writing and numeracy.
Assessing these things is notoriously difficult, however. It’s even harder to put numbers onto knowledge. That hasn’t stopped people trying to do just that, and since the National Curriculum was introduced in 1988 children have been assessed as being at different ‘levels’ based on what knowledge, skills and understanding various experts have said that they should have.
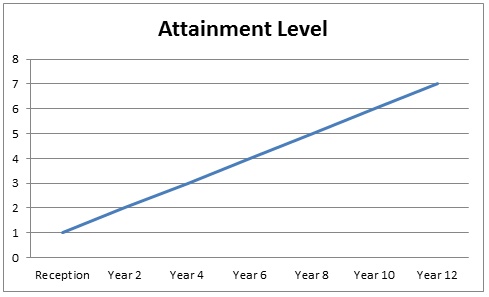
The levels were fairly arbitrary, as they had to be, since you can’t actually measure knowledge, skills and understanding using an absolute scale. The experts simply drew up a set of things that children should know and be able to use. As I understand it from Warwick Mansell’s Education by Numbers, Year 6 was allocated as Level 4, Year 2 as Level 1 and then a straight line graph was drawn as follows:
The government, in its wisdom, decided to produce ‘performance tables’ based on the data it began to collect. Teachers pointed out that having a small number of levels didn’t really give a good picture of what children could actually do. And schools pointed out that the differing levels of prior knowledge children had meant that a straight set of levels helped some schools and disadvantaged others. So sublevels were introduced, and measures of ‘value added’ were invented. Levels became ‘point scores’, and more numbers were used to try to picture what schools’ imperfect assessments were actually saying.
All this coincided with an era when computers have made processing data very easy, and it’s fairly obvious why those overseeing the running of schools took to data in big way. Unfortunately, it would appear that those collecting and analysing the data dumps from schools have very little understanding of the wonderful world of statistics and some extraordinarily bad analysis is now common place.
So, here are some problems with RAISEonline:
As noted above, you need to be fairly sure that your data is independent and identically distributed to use Z-scores and the like. If you want to test whether the test results for a given school is statistically significant when compared to a national mean and standard deviation, as RAISEonline does, you are effectively testing a ‘school effect’. Is there something about this school which makes it different to a control sample, in RAISEonline’s case all the children contributing results for a given school year?
So what does make the school different? Is it the quality of the teaching and learning, as RAISEonline implicitly assumes? Is it a particular cohort’s teaching and learning? Is it the socio-economic background of the children? Is it their prior attainment? Is it their family income? Or is it a combination of these factors?
All of this begs the question, what is RAISEonline actually assessing?
RISE, the Research and Information on State Education think tank, found that “School performance is strongly related to the prior attainment and socio-economic background of a school’s intake.” They also noted that “schools do not operate in a vacuum and some of the influences on pupil attainment, such as maternal health and wellbeing, family income, parental job security, the socio-economic mix of peers and access to thriving labour markets.”
So is RUBBISHOnline testing all of these things against a huge national sample which jumbles up all of this and loses all meaning?
The Not Independent and Identically Distributed problem
If you are testing the effect of a given fertiliser on a given species of plant, you can be fairly sure that each of the plants in a sample of plants is independent and identically distributed. This is complicated, but essentially, you should be able to swap any of your plants between sample groups before conducting your experiment, since any given plant should react to the experiment in the same way.
In order to be able to assume that a sample cohort which has supplied test results for a school is independent and identically distributed, you should be certain that a completely different random group of children subject to the same teaching and learning would perform in exactly the same way.
This seems entirely unlikely, since a given cohort in a given school will not be randomly selected from the entire population. The children are likely to be similar to each other in a statistically significant way - which could be socio-economic background, prior attainment, family income and so on. And that means that attainment levels of the cohort are not independent and identically distributed random variables.
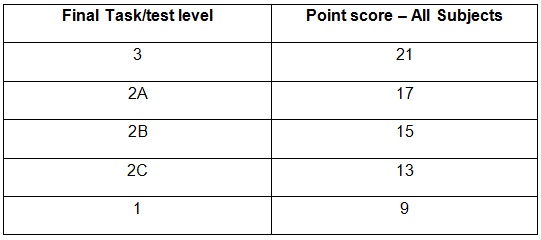
The Key Stage 1 Data Manipulation problem
At Key Stage 1, children can be assessed as being at Level 3, 2A, 2B, 2C or 1. These levels are given point scores – which you can find on page 55 of this document – as follows:
As a result of this, teachers have been forced to manipulate data. A child assessed at Level 3 is automatically assigned level 3B, likewise Level 1 is assigned 1B. This has hugely important implications later on, as progress measures are calculated using this initial, compromised, data.
Incidentally, there is a level 4+ category at KS1. Almost no child is ever assigned a Level 4B assessment at KS1, because schools have to show progress over a Key Stage, and no child can be assigned Level 7 at KS2, so it would never happen. There is also a W level – working towards level 1 – which is arbitrarily assigned 3 points. Why? Who knows? This category is for children who clearly have special educational needs, and is clearly not part of the mainstream.
So, a mainstream child can only be assigned to one of five categories, which are heavily subjective. At the more able end, the data is fudged because some children might be a little more advanced than 2A but not as much as 3B, and schools are forced to choose a category. At the lower ability end, a similar situation applies. The data has already been compromised before any analysis is undertaken.
The Primary Age problem
Age matters a great deal at Key Stage 1. Children are put into cohorts with a 365 day range. Some children are up to 13% younger than others in the same cohort when they are assessed. Given that children are likely to have been talking for just five years by the time they are assessed in May of Year 2, some have effectively 20% less experience than others in the same cohort. Remember that any analysis using Z-scores must assume that the data is independent of any underlying variable. KS1 data is heavily skewed by an underlying age factor.
Key Stage 2 is similarly influenced, since some children in Key Stage 2 are 8% or so younger than their oldest classmates, a huge twelve months behind in life experience and learning time.
The Loss of Definition Problem
Statisticians have always been very careful not to overstate what can and cannot be inferred when you start to manipulate data. As well as being rigorous about assumptions and independence of data, it has also been long recognised that the more you manipulate data, the more errors you should account for and the more you lose definition of your data.
For example, you might measure heights, ages and shoe size of a population, and then create a weighted average of those three measures. Any analysis using this new measure, let’s call it the Average Measure Score (AMS), would be a lot more general than the three specific measures on which it is based. Someone with particular AMS might look and be quite different to another person with the same AMS, because you have lost definition by combining three measures.
At primary level, RUBBISHonline combines three scores into an Average Point Score, which doesn’t actually mean anything when you think about it. You can’t tell whether someone with an APS of 13 was assessed at Level 1 for reading and writing and Level 3 for numeracy or whether they were assessed at Level 2c for all three. And because you can only score either 9, 13, 15, 17 or 21 points, lots of children will have an APS of 15 with a Level 2C, 2B, 2A or 1, 2B, 3 in any combination of subjects, for example. The APS becomes meaningless.
This gets worse at GSCE when five different numbers are combined into a single Average Point Score. What exactly does an APS of 390.8 mean?
The Missing Data Problem
RUBBISHonline allows children with missing data to be given an APS, so if you miss an assessment at KS2, you simply take an average of the other two assessments. The mind boggles, and APS becomes even more meaningless.
The Misunderstanding Significance Problem
If you’ve seen a RUBBISHonline report, you will have seen ‘Sig+’ and ‘Sig-‘ appearing here and there. It’s used incorrectly, or at least with no statistical justification worth its salt.
Now, in statistical theory, significance is a specific term, and it isn’t quite what you might think. It doesn’t mean ‘important’ as many people would legitimately infer. ‘Significance’ is the likelihood that something is not simply due to chance. So if you take a random sample of a population and find its mean, you would expect that mean to be slightly different to the mean of another sample of the same population. It might be bigger or smaller, but it would be expected to be similar.
What significance tests do is suggest – and that’s all they do – that one mean which is very different to another may be from a different population and that this is not simply by chance.
There is more to the idea of significance involving Null Hypotheses and Type I and Type II errors. I could go on about this at length, but I’ll simplify by saying that the starting point is usually to check whether something is likely to be within the 95% of possible values which would indicate that two samples are from the same population and to take it from there. Given that there is very little likelihood that a school cohort and all the children in the country of the same age are from the same population, there is little point trying to test for significance, since any statistician will tell you that they can't be compared that way anyway.
The RUBBISHonline Methodology Document suggests that ‘Significance is a statistical term that shows if a difference or relationship exists between populations or samples of data’. Which is not what significance means to statisticians at all. It might 'suggest', given all the caveats above, but it doesn't 'show' anything. Now, RUBBISHonline might say that they have used this explanation because their methodology document is aimed at the general reader; this won’t wash since there is enough higher level maths in the document which would be beyond most people. I understand the statistics and I am not in the least persuaded that those behind RUBBISHonline do.
The RUBBISHonline problems
I could go on (and on) about RUBBISHonline, but even this initial headline analysis shows why this stuff is, in fact, rubbish because of the 'What's it testing? problem, the Not Independent and Identically Distributed problem, the Primary Age problem, the Key Stage 1 Data Manipulation problem, the Loss of Definition Problem, the Missing Data Problem and the the Misunderstanding Significance problem.
And this is the data on which schools are judged by those who know no better
It’s worth quoting the following in full. It comes from the National Governor’s Association’s document Knowing Your School.
"The purpose of RAISEonline is twofold. Firstly, it is an important (but by no means the only) source of data for school governors to use in retrospective self-evaluation and school improvement planning. It should be used alongside other sources of data such as the Ofsted Data Dashboard, FFT Governor Dashboard, FFT Self Evaluation Booklet and the schools’ own pupil tracking data.
Secondly, the analyses are used by Ofsted inspectors during their inspection of schools. It is therefore critical that you are able to interpret your school’s data from an inspector’s perspective and can identify apparent areas of under-performance in order to explain why they occurred; or demonstrate that you recognise them and have set out the action you are taking to address them."
You are stuffed from the outset, as RUBBISHonline is likely to show up all kinds of warnings because it’s using the wrong, and incorrectly applied, tests of significance which don't even stand up to elementary statistical scrutiny. You'll be hammered by people using information supplied by nameless data wonks who have complete misunderstood the theories behind the sampling of data.
Variables and means have to be treated differently
A final, further, example of the sheer idiocy of the people who judge schools on RUBBISHonline data comes from yet another complete misunderstanding of the statistics of means of samples. Actual test marks can tell you things, and you can observe (with certain caveats, once again - statistics is not about certainty after all) a trend in the results which, say, a given child gets in tests. If a child gets 12, then 15 then 20 out of 30, there is a trend. Likewise, if they get 15, 15 and 15, or 20, 15 and 10.
But means don't work like that, because the central limit theorem states that they will be distributed normally. So the mean you have could be any one of any number of possible means. And you have to test if a given mean is significantly different from the mean which you might expect.
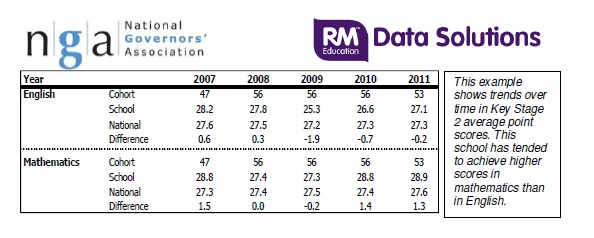
Not that those looking at data know this. For example, the NGA includes the following table in its guidance to governors:
But does it actually show this? The central limit theorum suggests that the mean of any sample could vary considerably and still be similar to another sample. A Z-test can be used to test whether the mean of a random sample is significantly different to the mean of another sample from the same population. Let’s look at one of these samples as reported in the table above – which aren’t random or independent as discussed above, but we’ll ignore that for now.
Let’s take Mathematics in 2007, because it’s got the biggest ‘difference’ – which is included in this table, illuminatingly, for reasons I’ll explain below. It has a mean APS of 28.8, for 47 children against a national mean of 27.3. Assuming that these are both samples from the population of children taking the key Stage 2 test. We are going to have to assume a standard deviation of 5.22 as in the Methodology document’s worked example for KS2 APS. Big assumption, but bear with me.
So, using the formula
Now, using the RUBBISHonline flawed methodology, this isn’t statistically significant. The two means can reasonably be assumed to have come from the same population. You might think that they are from different populations (which they are) because the value is really close to the line drawn for 'significant at the 95% level', but the theory says that they aren't.
I haven’t done the calculations for any of the other samples above, but I’m willing to bet that none of them are statistically significant. Which means that there is no ‘trend’ – they are all reasonable results if (big if) the school cohort is a representative sample of the population. By the way, the thing labelled ‘difference’ above is the kind of thing a complete non-mathematician would use. It’s entirely irrelevant if you understand statistical theory at A level standard. Which clearly very few people do.
So, should you ever have a conversation with anyone about RUBBISHonline - I don't know, an Ofsted inspector, or someone making judgements based on data - I suggest you ask them a simple question. "Can you explain your reasons for thinking that the data for our school reflects our school and no other factor and that it is independent and identically distributed?" If they can't answer that, then they are in no position to make any judgements using the data in the way they are trying to use it.
I doubt you will get anywhere, since the level of understanding of statistics - and trust me, this is entry level undergraduate stuff, it is not advanced weird barely-understood-by-anyone stuff - by those making judgements is utterly laughable.
And good luck with any attempt to “identify apparent areas of under-performance in order to explain why they occurred; or demonstrate that you recognise them and have set out the action you are taking to address them”. I doubt any Ofsted inspector will listen to your reasoned demolition of the statistical nightmare that is RAISEonline. If the people who have created the data analysis tools have so little understanding of what they are doing with data, what hopes are there that school inspectors do either? RAISEonline is deeply, deeply flawed and should be dismissed as such. It's RUBBISH.
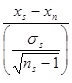
 RSS Feed
RSS Feed
